Correction - Évaluation non notée - Proportionnalité


a. La tour Eiffel mesure \(5{,}4~\textrm{cm}\) sur le dessin et on sait qu’elle mesure \(325~\textrm{m}\) en taille réelle.
Ainsi, l’échelle est donc de :
\(\displaystyle \textrm{échelle}=\frac{\textrm{taille dessin}}{\textrm{taille réelle}}=\frac{5{,}4~\textrm{cm}}{325~\textrm{m}}\)
\(\textrm{échelle}=\displaystyle\frac{5{,}4~\textrm{cm}}{32~500~\textrm{cm}}=\frac{1}{6250}\)
Remarque
Il faut bien faire attention à convertir les distances dans la même unité (ici le \(\textrm{cm}\)) avant de procéder au calcul. On n’hésitera pas à réaliser un tableau de conversion en cas de besoin (au brouillon ou sur la copie).
b. Sur le dessin, on mesure une hauteur de \(2~\textrm{cm}\). On peut donc écrire le tableau ci-dessous :
| Taille dessin | \(1\) | \(2\) |
|---|---|---|
| Taille réelle | \(6250\) | \(x\) |
On déduit donc que : \(\displaystyle{}x=\frac{2\times6250}{1}=12~500\).
La hauteur du 2e étage de la tour Eiffel est donc de \(12~500~\textrm{cm}\) soit \(125~\textrm{m}\).
Remarque
J’ai fait le choix de passer par un tableau de proportionnalité. Mais, le calcul d’une échelle est un "retour à l’unité". On aurait pu donc simplement effectuer l’opération suivante : \(6250\times2=12500~\textrm{cm}=125~\textrm{m}\)
a. On a une première augmentation de \(20~\textrm{\%}\), on calcule donc : \(2{,}2\times20~\textrm{\%}=\displaystyle2,2\times\frac{20}{100}=0{,}44\)
L’augmentation est donc de \(0{,}44~\textrm{\textrm{€}}\).
Le prix final est donc de : \(2{,}20+0{,}44=2{,}64~\textrm{\textrm{€}}\)
b. Le nouveau prix est de \(2,64~\textrm{\textrm{€}}\) puis, il subit une nouvelle hausse de \(20~\textrm{\%}\). Pour obtenir la nouvelle hausse, on calcule donc :
\(2,64\times20~\textrm{\%}=2,64\times\displaystyle\frac{20}{100}=0,528\)
Ainsi, le nouveau prix est donc de : \(2,64+0,528=3,168\approx3,17~\textrm{\textrm{€}}\)
Remarque
On arrondit le dernier résultat au centième près puisqu’il s’agit d’un prix et qu’on arrondit donc au centime.
c. Avec une augmentation de \(40~\textrm{\%}\) on aurait une augmentation de :
\(2,2\times40~\textrm{\%}=2,2\times\displaystyle\frac{40}{100}=0,88~\textrm{\textrm{€}}\)
On aurait donc un prix final de : \(2,2+0,88=3,08~\textrm{\textrm{€}}\)
Ce qui est inférieur au résultat trouvé en question b., donc l’augmentation est finalement supérieure à \(40~\textrm{\%}\) et non égal à \(40~\textrm{\%}\)
Remarque
On aurait pu aussi calculer l’augmentation à partir du résultat de la question b.. On aurait donc :
\(\displaystyle\frac{3,168}{2,2}=1,44=\frac{144}{100}=144\textrm{\%}\).
Ainsi, suite aux deux augmentations successives, le prix a augmenté de \(44~\textrm{\%}\).
a.
| Âge du fils | \(2\) | \(5\) | \(8\) | \(13\) | \(12\) |
|---|---|---|---|---|---|
| Âge de la mère | \(27\) | 30 | \(33\) | 38 | \(37\) |
b. Il y a plusieurs façons de démontrer que cette situation n’est pas une situation de proportionnalité :
Remarque
Une seule de ces trois justifications suffit.
a. On commence par calculer le prix d’un kilogramme de citrons : \(\displaystyle\frac{14}{5}=2{,}8\)
Le prix d’un kilogramme de citron est donc de \(2,8~\textrm{\textrm{€}}\).
La masse de citrons qu’on peut acheter avec \(18~\textrm{\textrm{€}}\) est de : \(\displaystyle\frac{5\times18}{14}\approx6{,}43~\textrm{kg}\)
b. 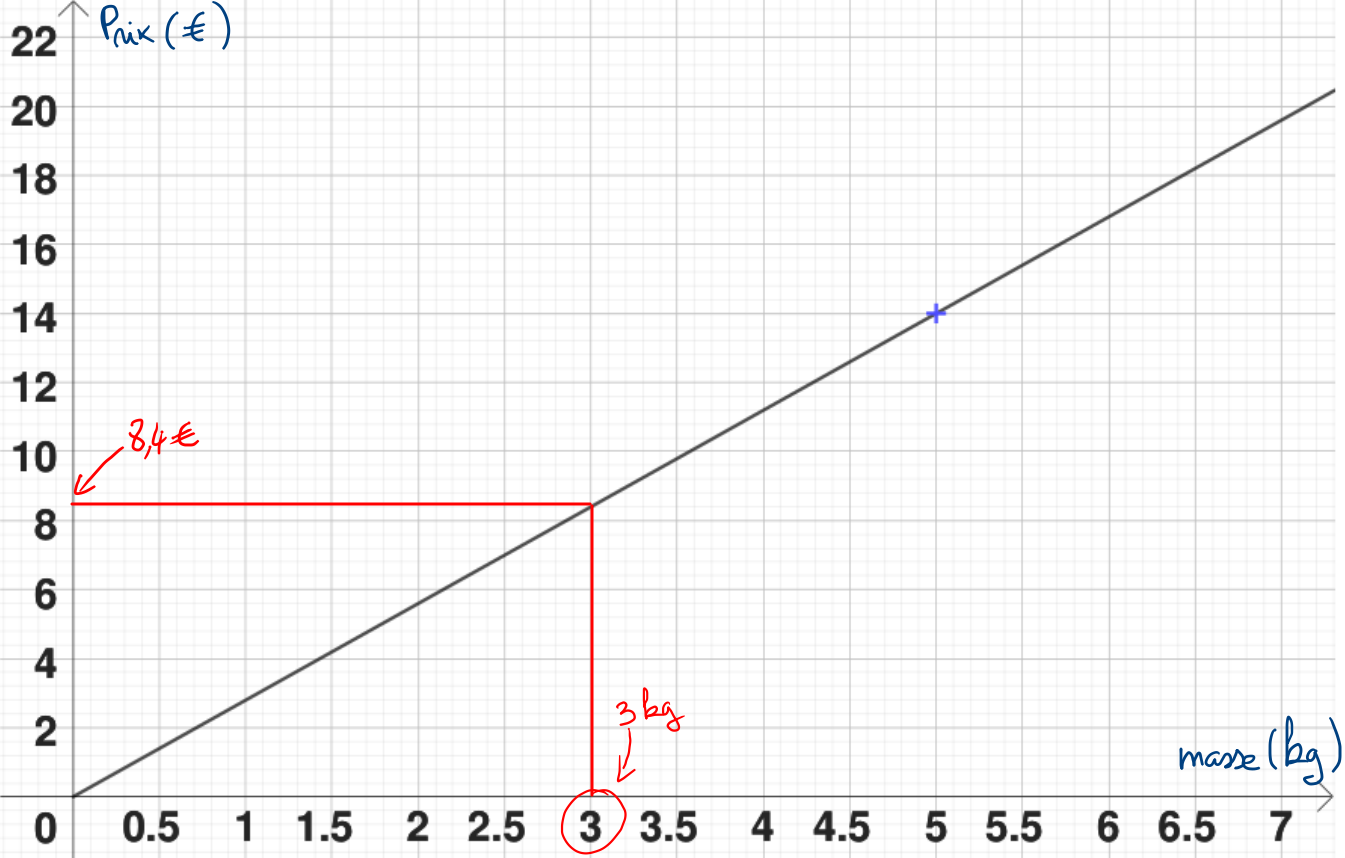
On lit graphiquement qu’on peut acheter \(3~\textrm{kg}\) de citrons avec \(8{,}4~\textrm{\textrm{€}}\).
c. On peut ajouter un colonne au tableau :
| masse citrons (\(\textrm{kg}\)) | \(1\) | \(5\) | \(\approx6{,}43\) | \(x\) |
|---|---|---|---|---|
| prix (\(\textrm{\textrm{€}}\)) | \(2{,}8\) | 14 | 18 | \(8{,}4\) |
Par le calcul, on a : \(\displaystyle{}x=\frac{5\times8{,}4}{14}=3\).
On retrouve bien qu’on peut obtenir \(3~\textrm{kg}\) de citron avec \(8{,}40~\textrm{\textrm{€}}\).
Remarque
J’ai fait le choix de prendre la colonne avec \(5~\textrm{kg}\) pour effectuer mes calculs puisque la valeur \(6{,}43~\textrm{kg}\) est une valeur approchée.
Les deux grandeurs étudiées au cours de cette exercice sont :
Pour cet exercice, on peut réaliser un tableau de proportionnalité, on prendra le \(\textrm{km}\) comme unité de distance et les \(\textrm{min}\) comme unité de temps.
Avant de le remplir, on réalise les différentes conversions nécessaires :
On sait que la voiture roule à \(84~\textrm{km/h}\), donc elle effectue \(84~\textrm{km}\) en \(1~\textrm{h}\) et donc elle réalise cette distance en \(60~\textrm{min}\).
| Distance (\(\textrm{km}\)) | \(84\) | \(147\) | \(210\) | \(75{,}6\) | \(58{,}8\) |
|---|---|---|---|---|---|
| Temps (\(\textrm{min}\)) | \(60\) | \(105\) | \(150\) | \(54\) | \(42\) |
On peut effectuer, les calculs à l’aide du produit en croix ou par un retour à l’unité.
Remarque
Pour la question b. on aurait pu aussi simplement calculer : \(84\times2{,}5=210~\textrm{km}\)
Puisque \(2~\textrm{h}~30~\textrm{min}=2{,}5~\textrm{h}\)
La figure est divisée en quatre carrés.
On remarque que la figure est symétrique par rapport au point central.
On va donc calculer l’aire de la surface colorée des deux carrés de gauche puis multiplier par deux le résultat.
\(\textrm{Aire du carré}=1\times1=1~\textrm{cm}^2\)
\(\textrm{Aire du quart de disque blanc}=\displaystyle\frac{\pi\times1^2}{4}\)
\(\textrm{Aire colorée}=\textrm{Aire du carré}-\textrm{Aire quart du disque blanc}\)
\(\textrm{Aire colorée}=1-\displaystyle\frac{\pi\times1^2}{4}\)
On utilise le résultat obtenu précédemment et on a :
\(\textrm{Aire colorée}=\textrm{Aire du quart de disque colorée}=\displaystyle\frac{\pi\times1^2}{4}\)
\(\textrm{Aire}=\displaystyle1-\frac{\pi\times1^2}{4}+\frac{\pi\times1^2}{4}=1~\textrm{cm}^2\)
Ainsi, l’ensemble de la figure a une aire de \(2~\textrm{cm}^2\) (en effet, on a : \(1~\textrm{cm}^2\times2=2~\textrm{cm}^2\)).
On remarque que la figure est composée d’un rectangle et d’un demi-disque.
On va calculer leur aire respective puis les sommer pour avoir l’aire totale.
\(\textrm{Aire du rectangle }=8\times12=96~\textrm{cm}^2\)
\(\textrm{Aire du demi-disque}=\displaystyle\frac{\pi\times4^2}{2}\)
\(\textrm{Aire du demi-disque}\approx25{,}13~\textrm{cm}^2\)
Remarque
Le diamètre est de \(8~\textrm{cm}\), le rayon est donc bien de \(4~\textrm{cm}\).
\(\textrm{Aire totale}\approx96+25{,}13\approx121{,}13~\textrm{cm}^2\)