1. Pour convertir une distance en \(\textrm{km}\) en \(\textrm{m}\), on peut réaliser le tableau de conversion\(~\):
| \(\textrm{km}\) | \(\textrm{hm}\) | \(\textrm{dam}\) | \(\textrm{m}\) | |
|---|---|---|---|---|
| \(1\) | \(9\) | \(6\) | \(0\) | \(0\) |
Et on a donc, \(19{,}6~\textrm{km}=19~600~\textrm{m}\)
2. Pour convertir des durées, on se souvient que : \(1~\textrm{min}=60~\textrm{s}\)
On a alors : \(21~\textrm{min}~18~\textrm{s}=21\times60~\textrm{s}+18~\textrm{s}=1278~\textrm{s}\)
Ainsi, le coureur cycliste a mis \(1278\) secondes pour parcourir \(19~600\) mètres.
3. Une vitesse moyenne est égale au rapport entre la distance parcourue et le temps écoulé.
On a alors : \(\displaystyle{}v=\frac{d}{t}\) \(~~~~\) où \(v\) est la vitesse, \(d\) est la distance et \(t\) est le temps.
On procède au calcul : \(\displaystyle{}v=\frac{19600~\textrm{m}}{1278~\textrm{s}}\approx{}15{,}33~\textrm{m/s}\)
4. Pour convertir une vitesse en \(\textrm{m/s}\) en \(\textrm{km/h}\), on se souvient que : \(1~\textrm{m/s}=3{,}6~\textrm{km/h}\)
On a alors
: \(15{,}33~\textrm{m/s}=15{,}33\times3{,}6~\textrm{km/h}=55{,}21~\textrm{km/h}\)
La vitesse moyenne du coureur cycliste lors de ce contre-la-montre était donc d’envrion \(55{,}21~\textrm{km/h}\).
Sur le dessin de la Tour Eiffel, on mesure une hauteur de \(4{,}7~\textrm{cm}\).
On mesure une hauteur pour le deuxième étage de \(1{,}7~\textrm{cm}\)
On sait que la Tour Eiffel a une hauteur de \(330~\textrm{m}\) (taille réelle).
\(~\)
Puisqu’il y a proportionnalité entre la taille sur le dessin et la taille réelle. On a :
| Taille dessin \(\textrm{(cm)}\) | \(4{,}7\) | \(1{,}7\) |
|---|---|---|
| Taille réelle (\(\textrm{m}\)) | \(330\) | \(x\) |
On en déduit alors : \(\displaystyle{}x=\frac{1{,}7\times330}{4{,}7}\approx119\)
Ainsi, la hauteur du deuxième étage est d’environ \(119~\textrm{m}\)
Analyse de l’énoncé :
\(143~\textrm{m}^3\) par seconde c’est le débit après l’augmentation de \(30~%{}\) à cause de la pluie. En proportion, le débit avant était de \(100~%{}\), avec les pluies il est passé à \(130~%{}\) (car \(30%{}\) de plus).
a. Le débit est de \(143~\textrm{m}^3\) par seconde après une augmentation de \(30~%{}\).
On a alors l’égalité suivante :
\(\displaystyle{}\frac{143}{130}=\frac{d}{100}~~~~\) On en déduit alors que : \(d=\displaystyle{}\frac{143\times100}{130}=110\)
Ainsi, le débit avant augmentation était de \(110~\textrm{m}^3\) par seconde.
Maintenant, le débit baisse de \(30~%\). C’est bien \(30~%{}\) du "nouveau" débit : \(143~\textrm{m}^3\) par seconde.
b. On calcule \(30~%\) de \(143~\textrm{m}^3~\): \(143\times{}30~%{}=143\displaystyle{}\times\frac{30}{100}=42{,}9\).
Le débit diminue donc de \(42{,}9~\textrm{m}^3\), on calcule alors\(~\): \(143-42{,}9=100{,}1\)
Finalement, le débit est donc de \(100{,}1~\textrm{m}^3\) par seconde.
a. On a le tableau suivant :
| Âge de la fille | \(1\) | \(3\) | \(7\) | \(15\) | \(13\) |
|---|---|---|---|---|---|
| Âge du père | \(24\) | \(26\) | \(30\) | \(38\) | \(36\) |
b. Plusieurs justifications possibles :
Remarque
Une seule de ces justifications suffisait. Le fait que les "\(13~\textrm{ans}\)" de la fille apparaissent après ses "\(15\) ans" n’est pas un argument en faveur ou en défaveur d’une proportionnalité entre les âges.
Deux grandeurs peuvent être proportionelles sans que leurs données soient présentées de façon chronologique (ou rangées par ordre croissant)
a. On complète le tableau.
Remarque
Le plus simple étant de réaliser un retour à l’unité : \(\displaystyle{}\frac{247{,}5}{5}=49{,}5\). Mais effectuer des calculs par "produit en croix" était aussi possible. 😉
| Euro (€) | \(1\) | \(5\) | \(8\) |
|---|---|---|---|
| Roupie Mauricienne (Rs) | \(49{,}5\) | \(247{,}5\) | \(396\) |
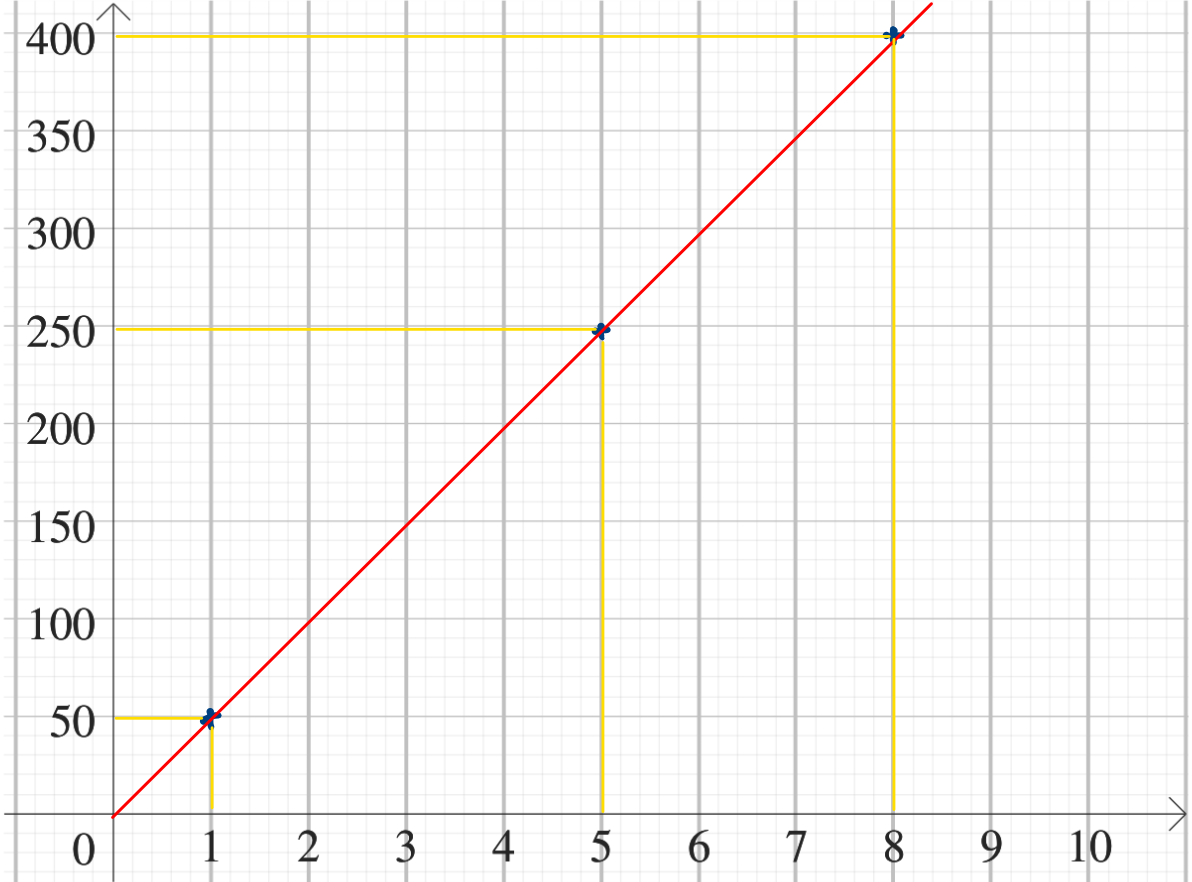
b. 
c. Les points sont tous alignés le long d’une droite qui passe par l’origine du repère. La situation représentée graphiquement est donc bien une situation de proportionnalité.