a.
Raisonnement
On nous demande de calculer \(BC\) ce qui serait possible si on connaissait \(AC\) grâce à l’application du théorème de Thalès dans les triangles \(ANM\) et \(ACB\).
On applique le théorème de Pythagore dans le triangle \(ADC\) et on a :
\(AC^2=AD^2+DC^2=4{,}8^2+6{,}4^2\)
\(AC^2=23{,}04+40{,}96=64\)
On en déduite donc :
\(AC=\sqrt{64}=8\)
\(AC\) a donc une longueur de \(8~\textrm{cm}\).
On remarque que :
On peut donc appliquer le théorème de Thalès et on les égalités suivantes :
\(\displaystyle\frac{AC}{AN}=\frac{AB}{AM}=\frac{BC}{MN}\)
Et en indiquant les valeurs des longueurs : \(\displaystyle\frac{8}{4}=\frac{AB}{AM}=\frac{BC}{3}\)
On trouve donc : \(\displaystyle\frac{8}{4}=\frac{BC}{3}\) et on en déduit finalement que \(BC=\displaystyle\frac{3\times8}{4}=6\).
La longueur \(BC\) est donc égale à \(8~\textrm{cm}\).
b.
Raisonnement
On veut démontrer que \(ABC\) est un triangle rectangle. On connaît : \(AB~=~10~\textrm{cm}\) (donné dans l’énoncé), \(AC~=~8~\textrm{cm}\) et \(BC~=~6~\textrm{cm}\) (calculés dans la question a.). On va appliquer la réciproque du théorème de Pythagore.
Dans le triangle \(ACB\), j’identifie le plus grand côté : \([AB]\). J’effectue des calculs séparés :
Je remarque que : \(AB^2=AC^2+BC^2\)
Par la réciproque du théorème de Pyhtagore, je conclus que le triangle \(ABC\) est rectangle en \(C\).
Remarque
On pourrait calculer la longueur \(AM\) de deux manières différentes :
- Avec le théorème de Thalès, comme pour la longueur BC.
- Mais aussi avec le théorème de Pythagore.
En effet, \((MN)\) et \((BC)\) sont parallèles, et \(BC\) est perpendiculaire à \((AC)\).
"Si deux droites sont parallèles, toute droite perpendiculaire à l’une est perpendiculaire à l’autre."
Ainsi, \((MN)\) est perpendiculaire à \((AC)\) et donc le triangle \(AMN\) est rectangle en \(N\).
Les éléments de réponse des questions : a., b. et c. sont présents sur la figure ci-dessous :

d.
Raisonnement
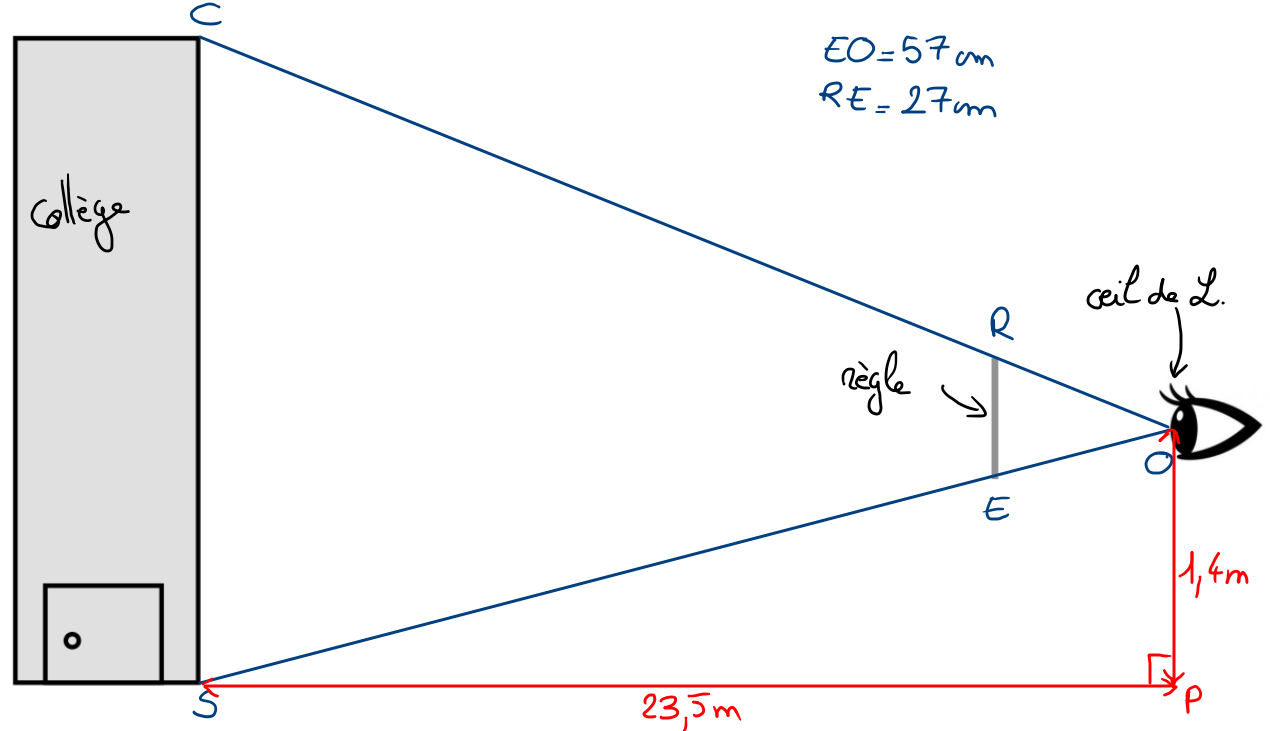
Pour calculer la hauteur du collège (c’est-à-dire la longueur \(CS\)), on voudrait appliquer le théorème de Thalès (en émettant l’hypothèse que les droites \((RE)\) et \((CS)\) sont parallèles).
Cependant, il nous manque la longueur \(SO\) puisque la distance qui a été mesurée est celle entre le collège et les pieds de \(\mathscr{L.}\) (et non son œil).
On va donc d’abord appliquer le théorème de Pythagore dans le triangle \(SPO\) puis appliquer le théorème de Thalès.
On applique le théorème de Pythagore au triangle \(SOP\) et on a :
\(SO^2=SP^2+PO^2=23{,}5^2+1{,}4^2=554{,}21\)
On en déduit que :
\(SO=\sqrt{554{,}21}\approx23{,}54\)
La longueur \(SO\) est donc de \(23{,}54~\textrm{m}\).
Remarque
On remarque que la valeur trouvée (\(SO=23{,}54~\textrm{m}\)) est très proche de celle mesurée au sol (\(SP=23{,}5~\textrm{m}\)). La première approximation faite en classe n’était donc pas absurde.
On émet l’hypothèse que :
On applique donc le théorème de Thalèse aux triangles \(COS\) et \(ROE\) et on a :
\(\displaystyle\frac{RO}{CO}=\frac{EO}{SO}=\frac{RE}{CS}\)
On remplace par les valeurs connues (on se souvient que \(SO\) reste une valeur approchée) et on a :
\(\displaystyle\frac{RO}{CO}=\frac{57~\textrm{cm}}{23{,}54~\textrm{m}}=\frac{27~\textrm{cm}}{CS}\)
Par précaution, on convertit toutes les longueurs en \(\textrm{cm}\) :
\(\displaystyle\frac{RO}{CO}=\frac{57~\textrm{cm}}{2~354~\textrm{cm}}=\frac{27~\textrm{cm}}{CS}\)
On en déduit finalement : \(CS=\displaystyle\frac{2~354\times27}{57}\approx1115~\textrm{cm}\approx11{,}15~\textrm{m}\)
La hauteur du collège est donc d’environ \(11{,}15~\textrm{m}\)