

a. \(Périmètre_{CATS}=4+6+4+6=20~\textrm{cm}\)
b. \(\textrm{Périmètre}_{\mathscr{C}}=2\times{}pi\times{}rayon\)
\(=2\times{}\pi\times3=6\pi~\textrm{cm}\)
c. \(Périmètre_{LYNX}=5+7+5+7=24~\textrm{cm}\)
d. \(Périmètre_{DOG}=5+6+5=16~\textrm{cm}\)
a. \(Aire_{CATS}=Longueur\times{}largeur\)
\(=4~\textrm{cm}\times6~\textrm{cm}=24~\textrm{cm}^2\)
b. \(Aire_{disque}=\pi\times{}rayon^2\)
\(=\pi\times(3~\textrm{cm})^2=9\pi~\textrm{cm}^2\)
c. \(Aire_{LYNX}=base\times{}hauteur\)
\(=7~\textrm{cm}\times4~\textrm{cm}=28~\textrm{cm}^2\)
d. \(Aire_{DOG}=\dfrac{base\times{}hauteur}{2}\)
\(=\dfrac{6~\textrm{cm}\times4~\textrm{cm}}{2}=12~\textrm{cm}^2\)
a. L’aire du terrain est constitué :
- d’un rectangle de \(20~\textrm{m}\) de longueur et \(10~\textrm{m}\) de largeur.
- d’un demi-disque de \(5~\textrm{m}\) de rayon
- d’un triangle rectangle à soustraire à cette surface d’une hauteur d’une longueur de \(4~\textrm{m}\) (\(10~\textrm{m}-6~\textrm{m}=4~\textrm{m}\)) et d’une base d’une longueur de \(3~\textrm{m}\)
(\(20~\textrm{m}-17~\textrm{m}=3~\textrm{m}\)).
\(Aire_{terrain}=Aire_{rectangle}+Aire_{1/2-disque}-Aire_{triangle}\)
\(=20~\textrm{m}\times10~\textrm{m}+\dfrac{\pi\times(5~\textrm{m})^2}{2}-\dfrac{3~\textrm{m}\times4~\textrm{m}}{2}\)
\(=200~\textrm{m}^2+\dfrac{25\pi}{2}~\textrm{m}^2-6~\textrm{m}^2\approx233{{,}}25~\textrm{m}^2\)
L’aire du terrain est de \(233{{,}}25~\textrm{m}^2\).
b. \(Aire_\textrm{maison}=11~\textrm{m}\times6~\textrm{m}=66~\textrm{m}^2\)
L’aire de la maison est de \(66~\textrm{m}^2\).
c. \(Aire_{jardin}=Aire_{terrain}-Aire_{maison}\)
\(Aire_\textrm{jardin}\approx233{{,}}25~\textrm{m}^2-66~\textrm{m}^2=167{{,}}25~\textrm{m}^2\)
L’aire du jardin est de \(167{{,}}25~\textrm{m}^2\).
a. Un sac de gazon permet de couvrir une surface de \(40~\textrm{m}^2\). On calcule donc :
\(\dfrac{167{,}25}{40}\approx4{{,}}18~\textrm{sacs}\)
Ainsi, il faudra alors \(5~\textrm{sacs}\) à M. Mat Grass pour qu’il puisse couvrir l’ensemble de son jardin.
b. Un sac coûte \(12{{,}}50~\textrm{\textrm{€}}\). On calcule :
\(12{{,}}50\times5=62{{,}}50~\textrm{\textrm{€}}\)
Finalement, M. Mat Grass devra payer \(62{{,}}50~\textrm{\textrm{€}}\).
Proportion de fauves au cirque Pandor : \(\dfrac{5}{12}\)
Proportion de fauves au cirque Zopoutou : \(\dfrac{11}{24}\)
Pour comparer deux fractions, on les écrit sous le même dénominateur et on a :
\(\dfrac{5}{12}=\dfrac{5\times2}{12\times2}=\dfrac{10}{24}<\dfrac{11}{24}\)
La proportion de fauve est donc plus importante au cirque Zopoutou qu’au cirque Pandor.
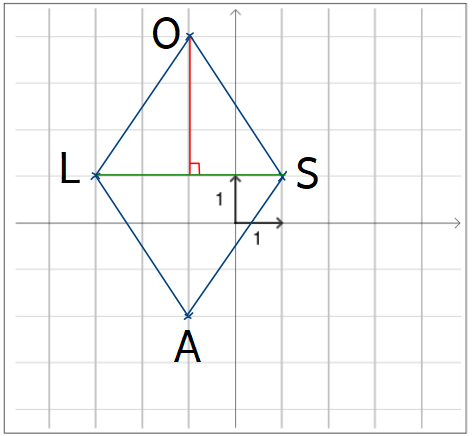
On peut partager le losange en deux triangles de d’aire égale, on peut donc calculer l’aire d’un premier triangle et la multiplier par \(2\).
\(Aire_{LOS}=\dfrac{base\times{}hauteur}{2}=\dfrac{4\times3}{2}=6~\textrm{u.a.}\)
\(Aire_{LOSA}=2\times{}Aire_{LOS}=2\times6=12~\textrm{u.a.}\)